Key Takeaways
As we all know, there is no such thing as free money. Whether you’re an investor or a household consumer, there will be occasions when you need to borrow funds for investments and purchases. The cost associated with borrowing money is called “interest.” As a borrower, you need to understand the difference between simple interest vs. compound interest, so that you know exactly how much borrowing money will end up costing you. This guide will break down simple and compound interest and the difference between the two types.
What Is Interest?
Interest is what you’re charged when you borrow money. Most commonly, you are assessed interest charges when taking out a loan from a bank or making purchases on a credit card. It is often expressed as APR, which stands for annual percentage rate. When taking out a loan, two main types of interest can be applied: simple interest or compound interest. Keep reading to find out the difference between simple vs compound interest.
[ Thinking about investing in real estate? Register to attend a FREE online real estate class and learn how to get started investing in real estate. ]

Simple Interest Vs. Compound Interest
There are two ways a financial institution will calculate interest: simple and compound interest.
-
Simple interest is calculated using only the principal amount of the loan.
-
Compound interest is calculated using the principal amount of the loan, plus the interest that has accumulated over previous periods.
The key difference between simple interest vs. compound interest is the amount of interest you’ll end up paying over the life of a loan. You can take its name as a hint; simple interest is easier to understand and calculate than its counterpart. Because you’re only paying interest off the principal amount of the loan, simple interest is the more affordable option for borrowers.
Compound interest will grow your outstanding balance quickly because your interest accrues its own interest. As a borrower, you’ll want to avoid compound interest as much as possible. For example, credit cards are associated with high annual percentage rates (APR) or interest that is compounded annually. Borrowers often find themselves in hot water when their interest seems to accrue faster than they can pay down the principal.
On the other hand, the fast growth rate associated with compound interest is great news for lenders and investors. It is a powerful tool for building wealth when you can use it to your advantage.
The following provides a few examples that demonstrate how simple and compound interest accrue differently:
-
Certificate Of Deposit: You have a $3,000 5-year CD that pays a simple interest of 1 percent. Over the 5 years, you would receive $150. If the CD was compounded monthly, you’d receive $153.75 instead.
-
Dividend Reinvestment: Let’s say that you purchased 100 shares of a company’s stock. The dividend is $3 per share. You would receive $300 in dividends, which you could reinvest to buy more shares. Over time, buying and owning more shares would compound your dividend payments.
-
Buy-and-hold Investment: The average annual stock market return is around 10 percent. If you committed to investing $300 every month for 10 years, compounded interest would help your portfolio grow to $58,152.85. With a total investment sum of $36,000, you would have made over $22,000 in interest.
[ Thinking about investing in real estate? Register to attend a FREE online real estate class and learn how to get started investing in real estate. ]
How To Calculate Simple Interest
Because simple interest is only calculated off of the loan principal, it’s easy to calculate. To calculate simple interest, use the following formula:
Simple Interest = P x r x n
In this case, the variable P is your principal amount, r is your annual interest rate, and n is the term of the loan, expressed in years.
All you have to do is take your loan principal and multiply it by your interest rate, and then multiply the resulting number by the number of years you are taking out the loan for. We’ll show you a couple of examples in the next section.
Simple Interest Examples
Example 1
Let us say that you are borrowing $10,000 from Bank A to finance an automobile purchase. You were quoted a simple interest rate of 5 percent, with a loan term of 5 years. The amount of simple interest you will pay, in addition to the principal of $10,000, will be $2,500:
$10,000 x .05 x 5 = $2,500
Example 2
In this next example, let us say you take out a personal loan toward your first home purchase from your family. They graciously lend you $40,000 at a 2 percent interest rate. They say you can pay it back slowly over the next 10 years. You will end up paying $8,000 in interest in this deal.
$40,000 x .02 x 10 = $8,000
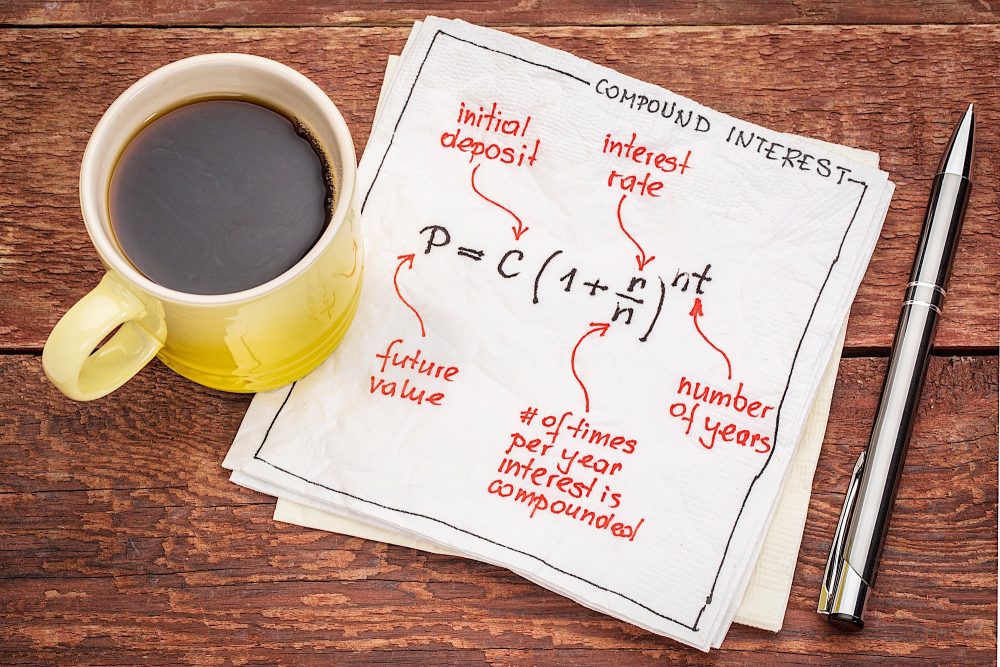
How To Calculate Compound Interest
Compound interest is a little more intricate than its counterpart, simple interest. Again, compound interest accrues and is added to any interest that was already accumulated in previous periods. In other words, the interest earns its own interest. The formula for compound interest looks like this:
Compound Interest = P[(1+r)^n – 1]
In the formula above, P is the total principal, r is the interest rate, and n is the length of the loan, expressed in years. You calculate compound interest by multiplying the loan principal by one plus the interest rate, which is raised to the number of years of the loan minus one. You can also put in a different compound period to find out how much compound interest you will have earned at any point in the loan period. It is much easier to explain how this formula works through concrete examples.
Compound Interest Examples
Example 1
Let’s use the same example from before so that you can see just how much compounded interest will magnify your repayment total. This time, you are taking out a $10,000 loan from Bank A, but the 5% interest rate is compounded. The loan term is still 5 years. In this case, you’ll end up paying back $2,762.82 in compounded interest. In the prior example, the simple interest was $2,500. The compounded rate increases your interest repayment by $262.82
$10,000[(1+.05)^5 – 1] = $10,000 (0.27628)
Example 2
Again, let’s go with Example 2 from above and switch out the simple interest rate with a compounded interest rate. Your family lends you $40,000, which can be repaid over 10 years. However, this time, they are asking you for 2 percent interest on this loan, to be compounded annually. Instead of an interest repayment of $8,000, it would be $8,759.78 when compounded each year. That is roughly $760 more than before.
$40,000[(1+.02)^10 – 1] = $40,000 (0.21899)
Important Compound Interest Concepts
There are a few important concepts when it comes to compound interest. These concepts help show how your money grows, what your compound interest is truly worth, and more. We’re going to go over the time value of money concept, as well as the Rule of 72.
Time Value of Money
The time value of money concept follows the general rule of “a dollar today is worth more than a dollar tomorrow”. The formulas to find the present value and the future value can be found below:
Present Value = Future Value / (1 + i)n
Future Value = Present Value x (1 + i)n
Legend:
i = Interest rate as a percentage
n = Number of compounding periods in a year
t = Total number of years for the investment
The Rule of 72
The Rule of 72 helps you determine when an investment will double in value. This formula requires you to input the rate of return or interest on the investment, and it also assumes that compounding is only done annually. Simply use the formula (72/interest) and you will have the answer to how many years it will take for your investment to double. For example, if your annual rate of return is 10%, your formula would be (72/10), equating to 7.2 years before your investment is doubled.
Compound Annual Growth Rate
Finally, let’s talk about the Compound Annual Growth Rate, or CARG. CARG is used when you need to find a single growth rate over a certain period of time. The best way to show you how this works is with an example calculation. For our example, we’ll say that your investment started out at $20,000 and it grew to $32,000 in a period of 10 years. To calculate our CARG, we would take the present value ($20,000), the future value ($32,000), and the amount of compounding periods (10). We then simply plug these numbers into our financial calculator or a spreadsheet and we’ll find the value of “i”. For this example, the value of “i” is 4.81%, meaning our annual rate of return was 4.81% on this investment.
Summary
As you learned from our examples above, it is very important to understand the difference between simple interest vs. compound interest. Compounded interest accrues much more quickly than simple interest, and can result in hundreds of additional dollars in interest repayment. As a borrower, compounded interest can work against you. However, keep in mind that you would enjoy its benefits if you can be on the investing or lending side instead. When finances are involved, it’s always a good idea to analyze the pros and cons and understand what you’re getting yourself into.
Ready to start taking advantage of the current opportunities in the real estate market?
Click the banner below to take a 90-minute online training class and get started learning how to invest in today’s real estate market!




